勾股定理的证明、推广及教学

李文革

勾股定理在数学发展史上的重要地位使其成为初中数学教育中开展探究活动、渗透数学文化的重要素材。勾股定理对培养学生的几何直观、推理能力和应用意识等数学核心素养具有重要作用。勾股定理不仅有许多巧妙的证法，而且还有许多形式的推广。

一、勾股定理的呈现形式及其证明

1. 勾股定理的呈现形式

（1）初中数学教材中的呈现形式

勾股定理在初中数学教材中的呈现形式如下：

直角三角形两直角边的平方和等于斜边的平方。

如图1，在△ABC中，∠C=90°，∠A、∠B、∠C对应的边长分别为a、b、c，则c2=a2+b2。

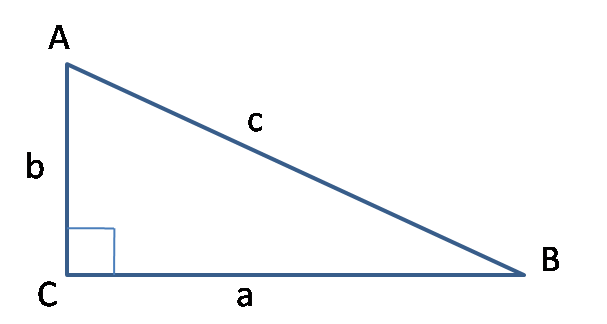
图1

（2）《几何原本》中的呈现形式

勾股定理在《几何原本》中的呈现形式如下（第1卷第47个命题）：

在直角三角形中，以两条直角边为边长的两个正方形的面积之和等于以斜边为边长的正方形的面积。

其标准图形如图2所示。

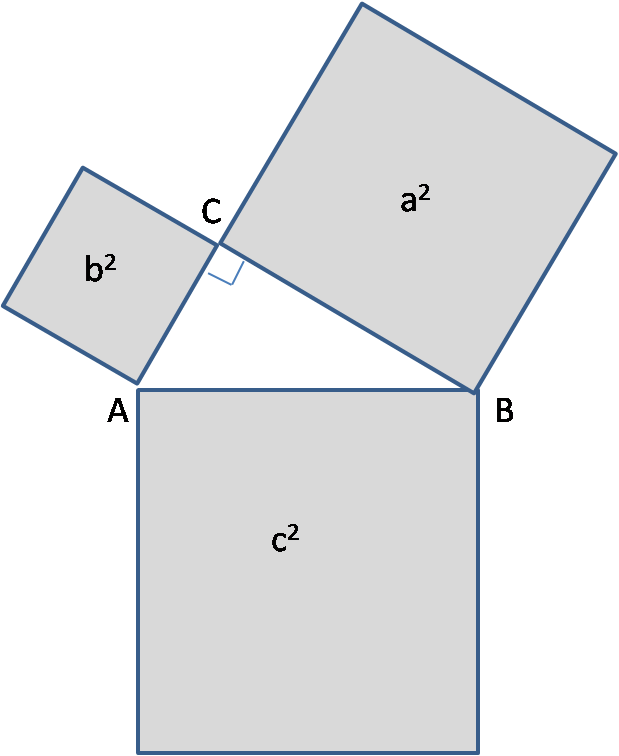
图2

2.勾股定理的证明

千百年来人们对勾股定理给出了多达三四百种证明，它是证明方法最多的定理。这些证明既验证了勾股定理，又大大丰富了研究问题的思想和技巧。中国古代学者赵爽、刘徽、梅文鼎、李潢、李锐、项名达、李善兰、华蘅芳等人都给出过勾股定理的证明；意大利文艺复兴时期的著名画家、雕刻家、建筑师达·芬奇也给出过勾股定理的证明；美国第20任总统茄菲尔德也给出过勾股定理的证明……在数百种证明方法中，有的十分精彩，引人深思；有的十分简洁，耐人寻味；有的因为证明者身份的特殊而非常有名。下面举出几种证明方法以示说明。

（1）利用“相似三角形”证明

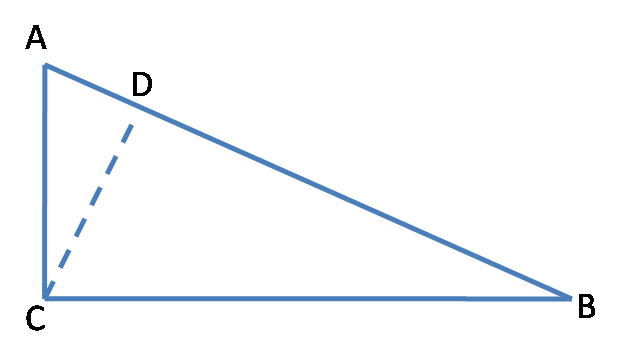
图3

（2）通过作内切圆证明

如图4，在Rt△ABC内作内切圆，设其半径为r，则

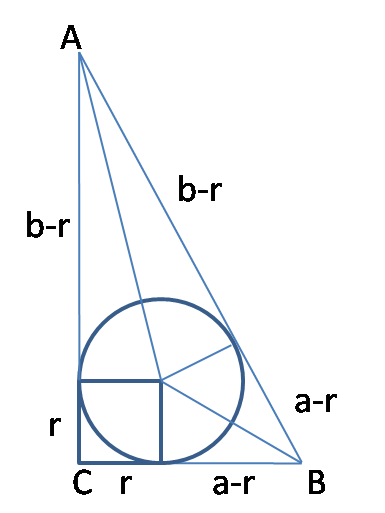
图4

（参见蔡宗熹. 千古第一定理——勾股定理[M]. 北京：高等教育出版社，2013）

二、勾股定理的二维和三维推广

1.二维推广

在用相似证明勾股定理时，根据“相似三角形面积的比等于相似比的平方”可以更简单地得到证明。

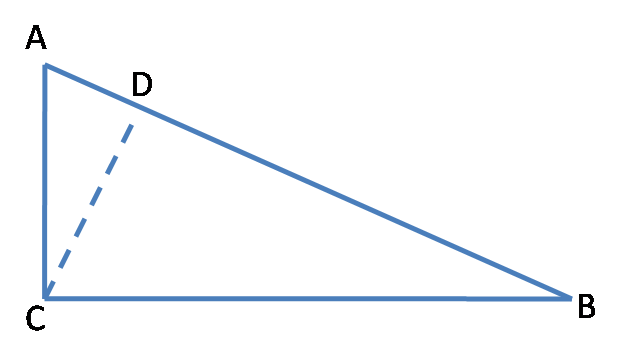
图5

受上述证明启发，我们可以发现一个很有趣的现象：

如图6，沿着Rt△ABC的斜边AB向上折叠，得到一个相同的三角形，其面积记着S1（就是Rt△ABC的面积）。再分别以AC、BC为斜边，向Rt△ABC的外部作与Rt△ABC相似的两个直角三角形（其面积分别记着S2、S3），再分别沿着AC、BC向内折叠，这两个直角三角形刚好填满Rt△ABC！即S1=S2+S3。

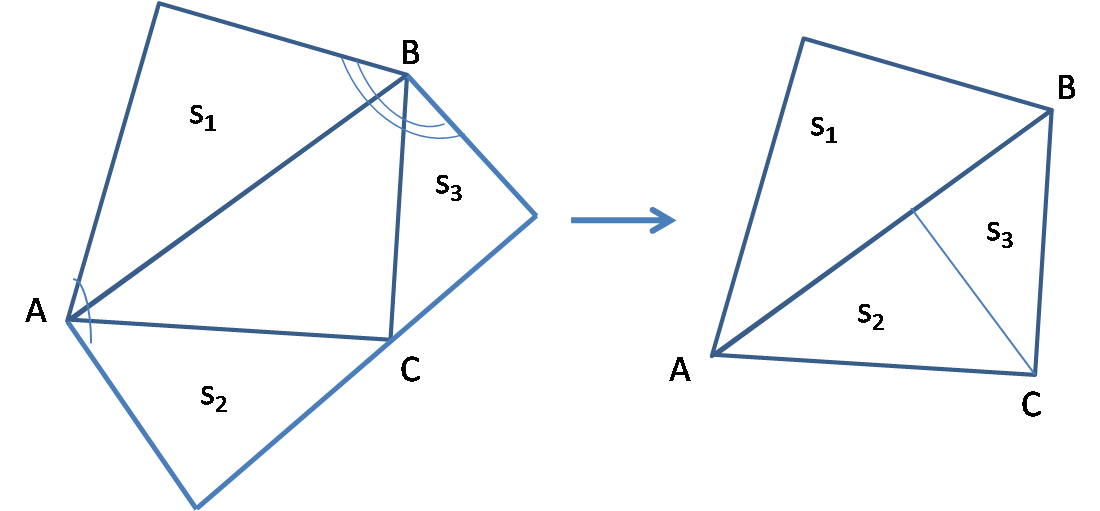
图6

这表明：

分别以直角三角形的三边为斜边作三个相似的直角三角形（如上述作法），则斜边所在的三角形的面积等于两条直角边所在的两个三角形的面积之和。

这可以看成是《几何原本》中勾股定理呈现形式的推广。类似地，我们还可以做如下推广：

推广1：如图7，在△ABC中，∠C=90°，分别以AB、BC、CA为边向形外作正三角形，其面积依次为S1、S2、S3，则S1=S2+S3。

【证明】

因为正三角形都相似，

所以S1：S2：S3= AB2 ：CB2：AC2。

而AC2+CB2 =AB2，

所以S1=S2+S3。

推广2：以直角三角形的直角边为边长的两个正n边形的面积之和，等于以斜边为边长的正n边形的面积。

因为正n边形都相似，与上面的证明类似，可知结论成立。这样我们可以得到更一般的推广3：

推广3：在分别以直角三角形三边各为一边的三个相似多边形中，以两条直角边为一边的两个多边形的面积之和等于以斜边为一边的多边形的面积。

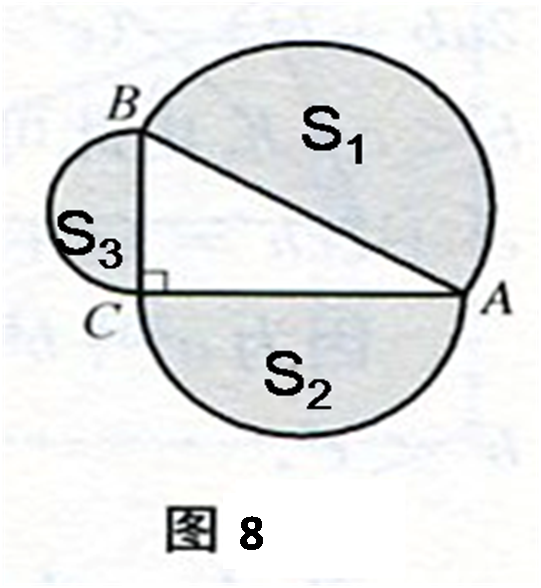
推广4：如图8，分别以Rt△ABC的三边AB、BC、AC为直径，向三角形外作三个半圆，则S1=S2+S3。

【证明】

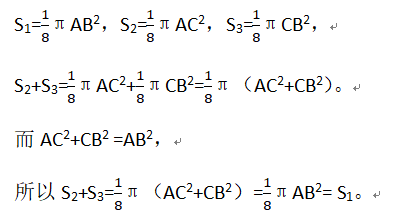
半圆都相似，这样我们可以得到更一般的推广5：

推广5：在分别以直角三角形三边各为一边的三个相似图形中，以两条直角边为一边的两个图形的面积之和等于以斜边为一边的图形的面积。

我们还可以把勾股定理推广到任意的三角形，得出余弦定理：

在△ABC中，∠A、∠B和∠C的对边分别为a、b、c，则

a2=b2+c2-2bccosA，

b2=c2+a2-2cacosB，

c2=a2+b2-2abcosC。

证明：如图9，设△ABC中，∠A为锐角，作CD⊥AB于点D，则据勾股定理有

a2-b2=(CD2+BD2)-(CD2+AD2)

=BD2-AD2

=(BD+AD)(BD-AD)

=c(c-2AD)

=c2-2cAD

=c2-2bccosA，

所以a2=b2+c2-2bccosA。

当A为钝角时（此时cosA＜0），同理可证上述等式也成立。

其他两式可同理证明。

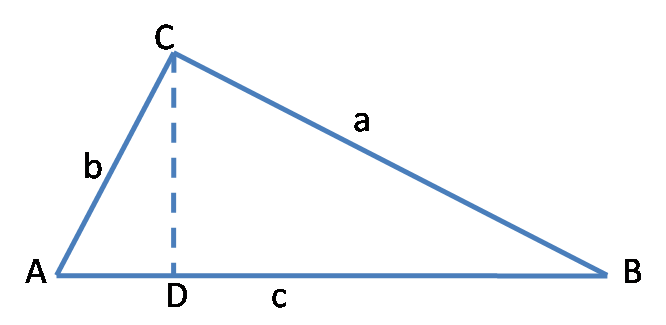
图9

2.三维推广

勾股定理和余弦定理分别可以推广至三维空间的情形。

三维空间的勾股定理：如图10，在直三棱锥D-ABC（D-ABC系直三面角）中，设S1、S2、S3、S4分别为△ABD、△BDC、△ADC和△ABC的面积，则S42=S12+S22+S32。

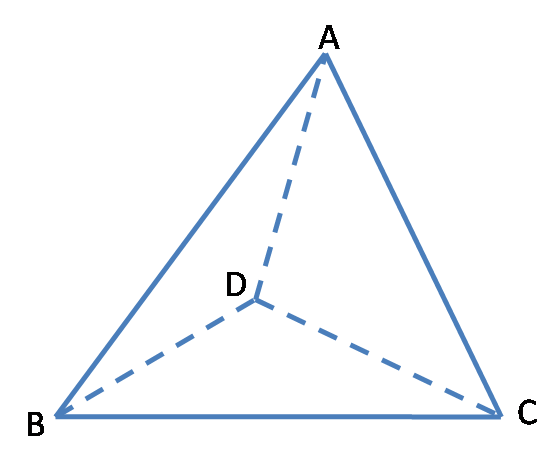
图10

三维空间的余弦定理：如图11，在三棱锥A-BCD中，设S1、S2、S3、S4分别为△ADC、△ADB、△BDC、和△ABC的面积，又二面角B-AD-C=α，A-BD-C=β，A-DC-B=γ，则

S42=S12+S22+S32-2 S1S2cosα-2 S2S3cosβ-2 S1S3cosγ。

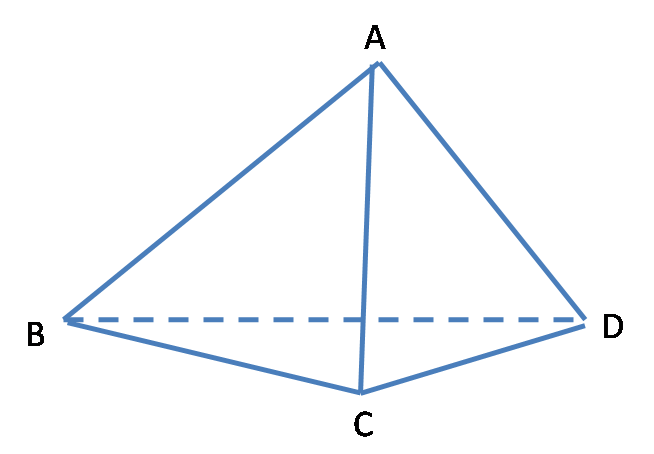
图11

三、勾股定理与费马大定理

勾股定理用方程式表示，就是：

x2+y2=z2。

满足这个不定方程的正整数解有无穷多个。

大约1637年左右，法国学者费马在研究丢番图《算术》一书的第2卷时，被毕达哥拉斯三元数组的种类和数量之多吸引住了。他进一步考虑：如果方程x2+y2=z2中未知数的幂次不是2而是3，这时方程还有正整数解吗？如果未知数的幂次是4呢？一般地，不定方程

xn+yn=zn（n＞2）有没有正整数解呢？

费马认为：方程xn+yn=zn（n＞2）没有正整数解。

这就是著名的费马大定理。

自从这一论断公诸于世后，一代代数学家以各种不同的方法尝试证明费马大定理，但都没有成功。在1637～1840年的200年间，人们只证明了当n为3、4、5、7这些值时费马大定理成立。

人们注意到两个简单的事实：

（1）如果当n=m时，方程没有正整数解，则当n=km（k为正整数）时也没有正整数解。

（2）只需考虑n为大于2的奇素数和n=4的情形。

1840～1850年间，高斯的学生、德国数学家库默尔用他创立的理想数理论对一批指数n证明了费马大定理：对于100以内除了37、59、67之外的所有奇素数p费马大定理成立。

此后，数学家们将奇素数p的取值逐步改进，借助计算机，截止1993年已经证明了当奇素数p＜400万时，费马大定理成立。继续沿着这样一条路走下去，虽然可以进一步改进奇素数p的取值，但永远也不可能彻底解决问题。必须开辟一条新路，才有可能达到胜利的彼岸。

1922年，英国数学家莫德尔提出了莫德尔猜想。按照莫德尔猜想，方程xn+yn=1（n≥4）至多有有限多个有理数解。但由方程xn+yn=zn的任意一组非零整数解都可以导出方程xn+yn=1的一组有理数解，因此，只要能够证明莫德尔猜想，就可以断言：如果xn+yn=zn（n≥4）有非零整数解（无公因子）的话，它至多只能是有限多个。1983年，29岁的德国数学家法尔廷斯证明了莫德尔猜想，并因此获得1986年的菲尔兹奖。

与从费马到法尔廷斯等前人不同的是，最后攻克顶峰的武器，综合利用了现代数学许多分支的成就，特别是1950年以来算术代数几何领域中关于椭圆曲线的深刻结果。

1995年5月《数学年刊》刊出了英国数学家怀尔斯的“模椭圆曲线与费马大定理”和泰勒与怀尔斯共同撰写的“某些Hecke代数的环论性质”的论文，从而宣告困扰人们三个世纪之久的费马大定理得到彻底解决。1996年3月，怀尔斯获得沃尔夫奖，成为获此殊荣的最年轻学者。

从费马大定理的证明过程我们可以看出：数学每前进一步，都是一代又一代数学家接续奋斗的结果。

（参见周明儒. 费马大定理的证明与启示[M]. 北京：高等教育出版社，2007）

四、勾股定理的教学

综上，我们可以将关于勾股定理的推广归纳为如图12所示。

图12

（参见吴振奎，吴旻. 数学的创造[M]. 上海：上海教育出版社，2006）

勾股定理的教学仅仅让学生知道结论并会套用是远远不够的，应让学生通过勾股定理的学习更好地掌握数学思想方法、激发学习兴趣、培养探索精神、经受历史的熏陶。

勾股定理蕴含着丰富的文化元素。教学中应通过介绍古代中国对勾股定理的发现、证明和使用的贡献，激发学生的民族自豪感。勾股定理曾先后在不同地区或国家被不同民族所发现，往往成为一种标志性的文化事件而载入这些地区或国家的文明史。为了促使学生更好地从多元文化视角看待数学，在教学中可以适当介绍勾股定理历史的国外素材。在历史上，不同国家不同行业的人士都研究过勾股定理的证明，这些人士包括数学家、艺术家、政治家等。教学中应适当增加论证思路的种类，丰富学生关于勾股定理论证思路的数学知识，同时将有关人士的证明方法纳入教学中，也可以为学生树立数学学习的榜样。

在勾股定理的教学中，要把握勾股定理在整个数学大厦中的地位和作用，关注勾股定理这一内容与相关数学知识之间纵向及横向的逻辑关系，把勾股定理的教学贯穿于整个初中数学教学的全过程，内容的展开遵循循序渐进和螺旋上升的原则，使勾股定理的教学成为一个统领数学知识的有机的整体，适时地将数学探究活动、数学文化融入课程内容，整体设计习题等课程资源。

在教学中通过设计探究活动，引导学生发现勾股定理并探究勾股定理的证明，增强学生的“发现感”，强化学生的主体性和探究性，使勾股定理的教学成为再创造和再发现的教学，进而发展学生发现、提出问题与分析、解决问题的能力。