平面的镶嵌

李文革

平面的镶嵌是指用一种图形或多种图形无缝隙、无重叠地铺满平面。据说早在毕达哥拉斯时代就开始了对这一问题的研究。华东师大版初中数学教材在七年级下册第88～92页对这一问题进行了简单研究。

一、用正多边形铺满平面

1.用单一的正多边形铺满平面

正n边形的内角和为（n－2）180°，它的每个内角的度数为（n－2）180°/n。如果它能铺满平面，则存在正整数m，使m（n－2）180°/n＝360°，即

m（n－2）＝2n。

解得n＝2＋4/（m－2）。

由于n为正整数，因此m＝3、4、6。这时n＝6、4、3，即只有正三角形、正方形、正六边形才能铺满平面。如图1是用正六边形铺满平面的情况。

图1

2.用多种正多边形铺满平面

对于给定的几种正多边形，它能否拼成一个平面图形，是看它们的内角加在一起能否组成一个周角，而我们可以利用多边形的内角和定理求出正多边形的内角。

设围绕某一点需要m块正多边形材料填充平面，则3≤m≤6。

求上述（1）～（4）四个方程的正整数解可得如下表所示的17种情况。

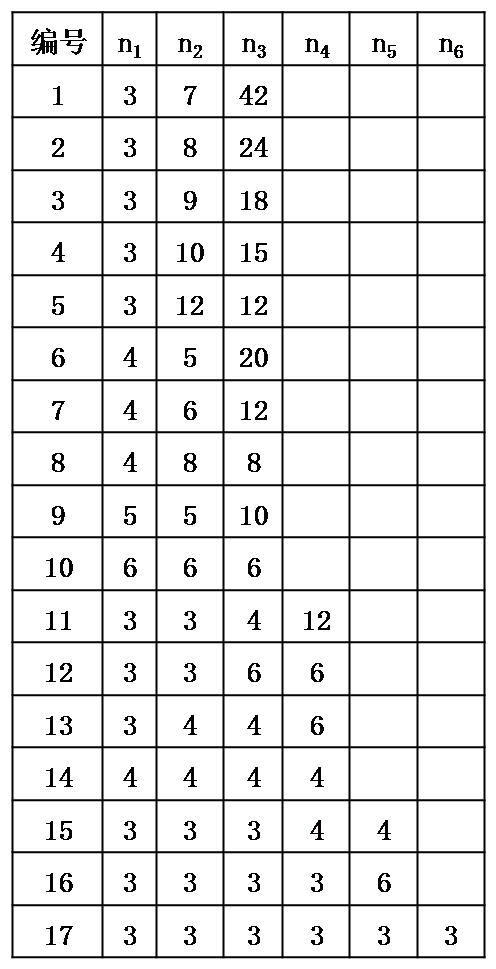
其中，第10、14、17种情况就是我们在“用单一的正多边形铺满平面”中讨论的三种情形，它表明只有正三角形、正方形、正六边形能填充平面。第1、2、3、4、6、9种情况不能填充平面。剩下的情况都能填充平面。

第5种情况如图2（1）所示；第7种情况如图2（2）所示；第8种情况如图2（3）所示；第11种情况如图2（4）所示。

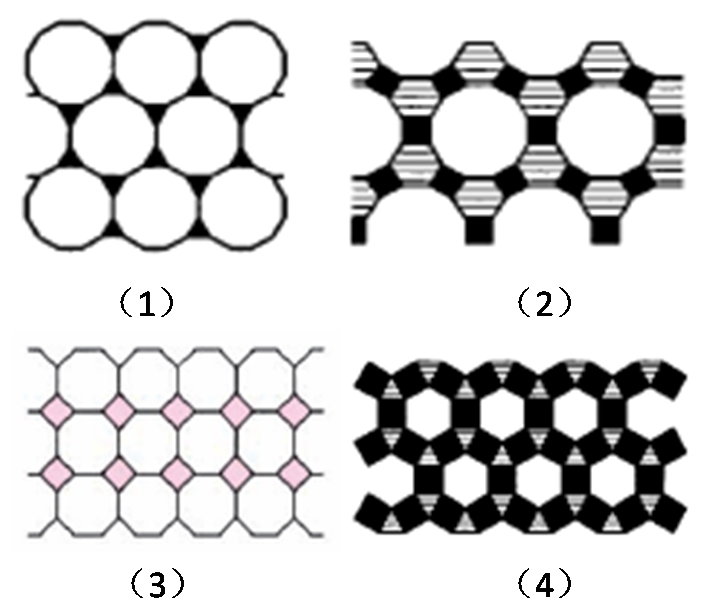
图2

第12种情况如图3（1）所示；第13种情况如图3（2）所示；第15种情况如图3（3）所示；第16种情况如图3（4）所示。

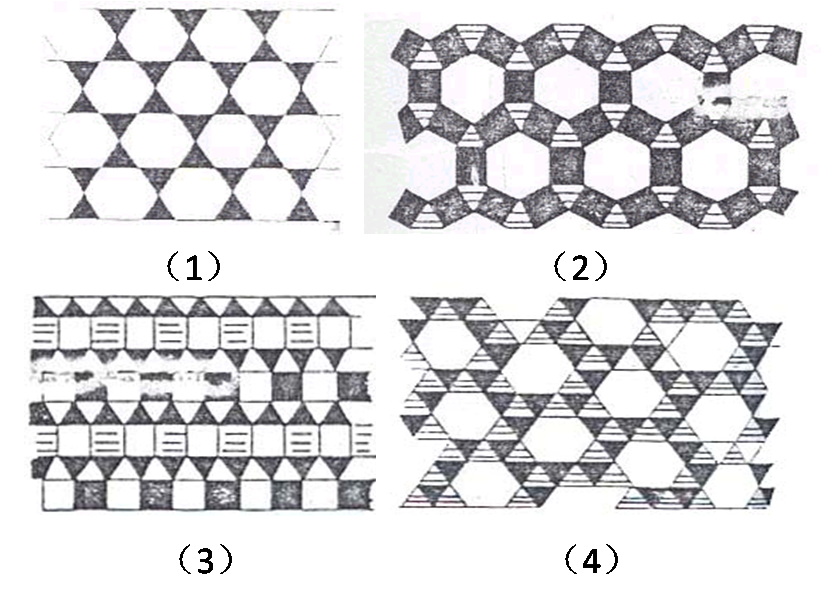
图3

二、用任意一种凸多边形铺满平面

1.用任意三角形

用任意两个相同的三角形均可以拼成一个平行四边形。如图4所示，平行四边形显然可以铺满平面。所以用任意的一种三角形均可以铺满平面。

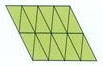
图4

2.用任意四边形

如图5所示，用任意一种四边形均可铺满平面。

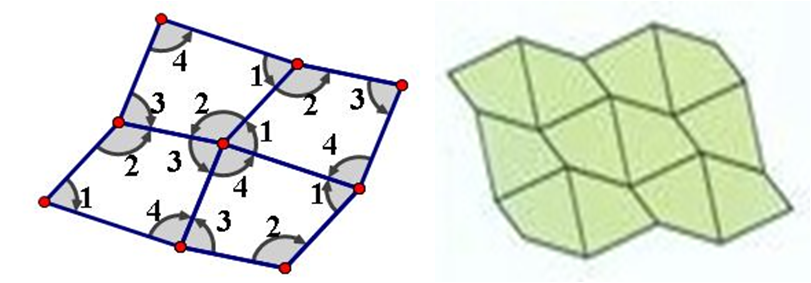
图5

3.用任意五边形

并非所有的五边形都能铺满平面。如图6所示，迄今为止人们已找到15种能铺满平面的五边形。

图6

2015年美国华盛顿大学数学家运用计算机程序，发现了如图7所示的第15种可以实现无缝拼接的凸五边形，它铺满平面的情形如图8所示。

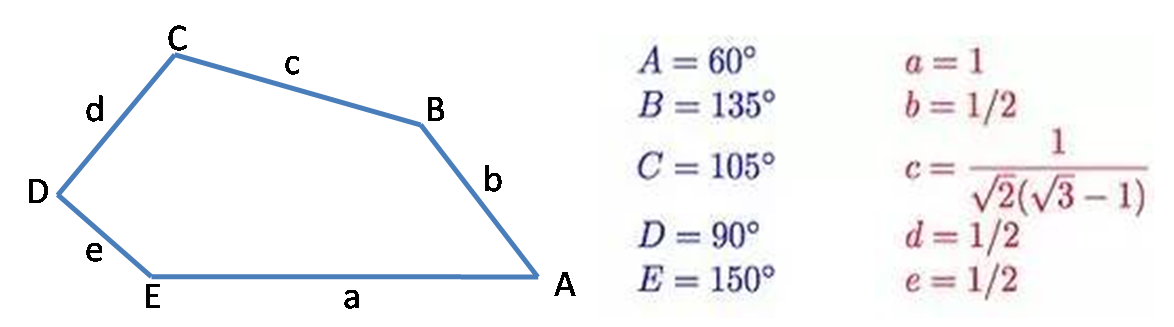
图7

图8

4.用任意六边形

迄今为止人们仅仅找到为数很少的几种能铺满平面的任意六边形，其中的一种如图9所示。

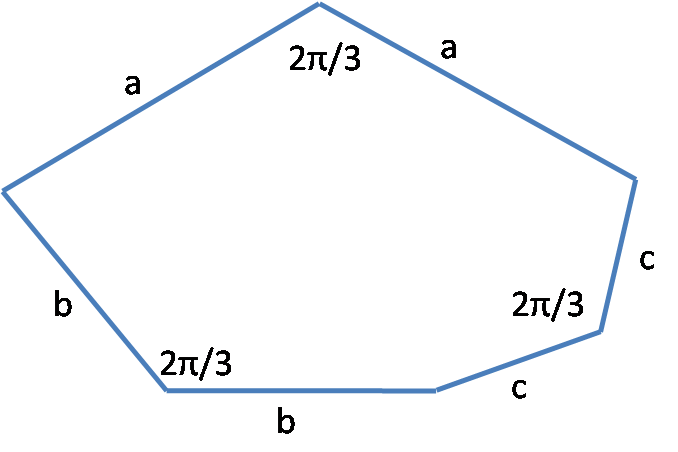
图9

三、用不规则图形铺满平面

1.用单一的不规则图形铺满平面

如图10就是用单一的不规则图形铺满平面的情形。

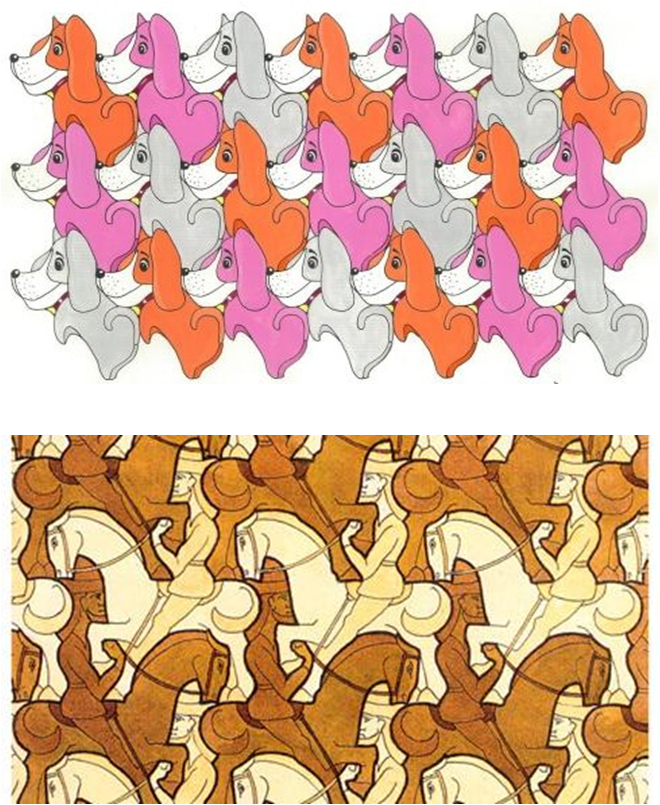
图10

2.用多种不规则图形铺满平面

（本部分参见：吴振奎，吴旻. 数学中的美[M]. 上海教育出版社，2004：292-295）

20世纪70年代，英国物理学家彭罗斯发表了他关于平面镶嵌的研究结果，他确定了如下三类瓷砖（下称彭罗斯瓷砖）：

如图11，第一类两种分别为风筝形和镖形，它们是由同一个菱形剪出的。

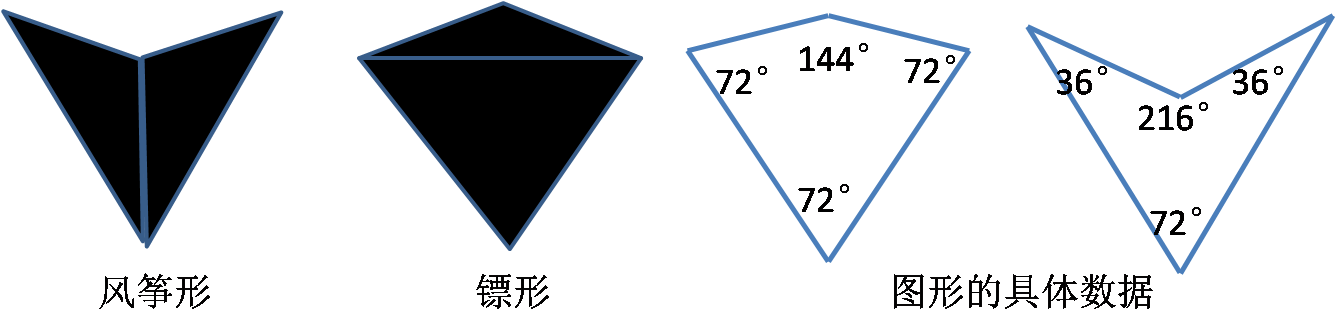
图11

如图12，第二类是由边长相同、胖瘦不一的两种菱形组成的（有趣的是它们面积比恰为）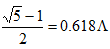

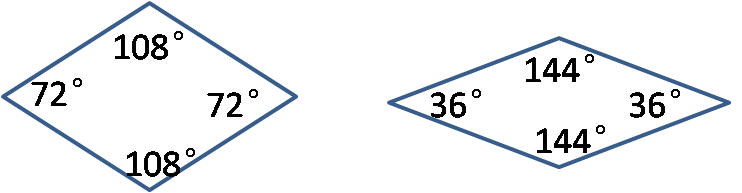
图12

如图13，第三类则由四种图形组成。

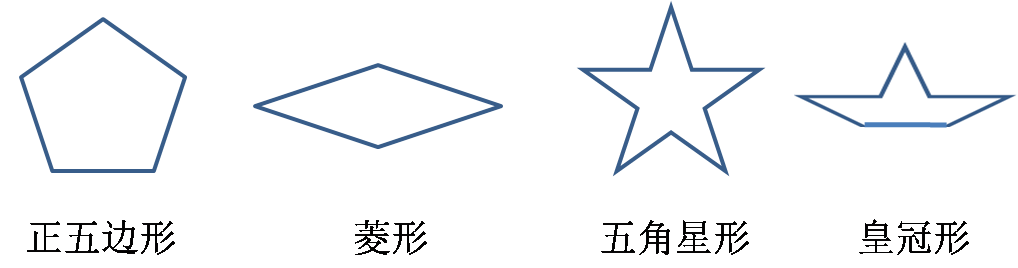
图13

有趣的是这三类瓷砖皆与正五边形（或五角星）有关：这些图形中的角要么是108°（正五边形内角），要么是72°（正五边形外角），要么是它们的一半或倍数：36°、144°、216°…

又如第一类的风筝形与镖形是由一个内角为72°的菱形依照五角星对角线长来分割而成的，即如图14（1）、（2）中AE、DE对应相等或比值相等。

图14

如图15，用它们中的每一类皆可铺满平面，同时铺设结构不具“平移对称性”，也就是说从整体上看图形不重复。

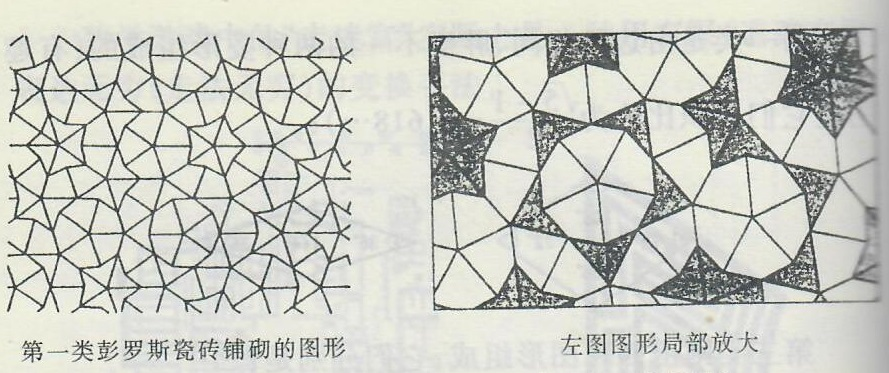
图15

用第二、三类彭罗斯瓷砖可铺砌成如图16所示的图形。

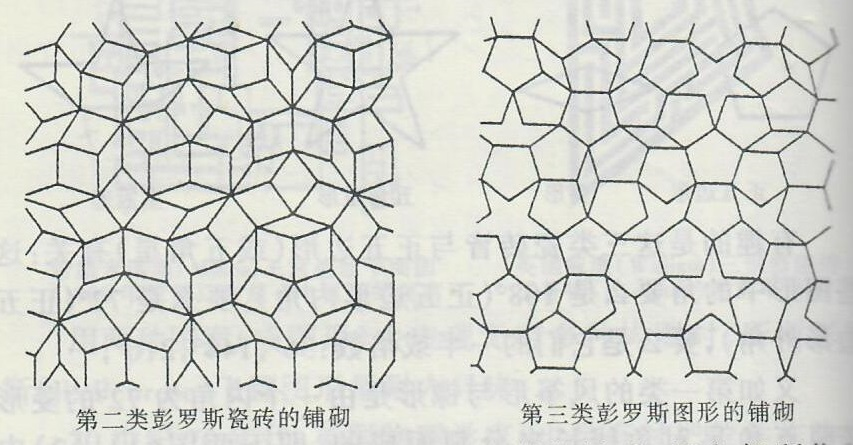
图16

利用彭罗斯瓷砖进行铺砌时，还可从铺砌的图形中，找出上述瓷砖自身的“克隆”，比如用第三类瓷砖的铺砌中（图17（1）所示）总可以找到它们的放大图形（图17（2）中粗线表示）。

图17