有趣的幻方
2018-09-05
有趣的幻方
李文革
华东师大版初中数学教材在七年级上册第8页用一个“阅读材料”简单介绍了幻方。幻方是一种数学游戏,如图1左,它最早出现于我国公元前2200年的“洛书”。
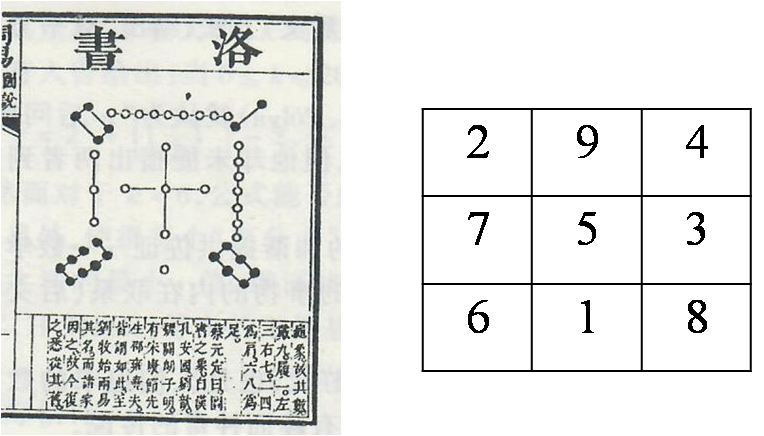
图1
“洛书”用数字表示就是如图1右所示的幻方,它的行、列及两条对角线上的数字和均相等,都等于15。
一、幻方是什么
幻方是一个方形,它每边含有相同数目的格数,每边的格数称为它的阶。“洛书”就是一个三阶幻方。如果是4行4列的方格组成的幻方,我们称之为4阶幻方,依次类推可以定义各阶幻方。幻方的行、列及两条对角线上的数字和均相等,称之为“幻和”。例如,如图1右所示的三阶幻方的幻和就是15。
不仅数学家研究幻方,物理学家、政治家也研究幻方。例如,美国政治家富兰克林(B.Franklin)曾制作了如图2所示的八阶幻方。它的幻和是260,它有一些独特的性质,如从16到10,再从23到17所成折线上八个数字之和也为260,且平行这种折线的诸折线上的八个数字之和也为260。
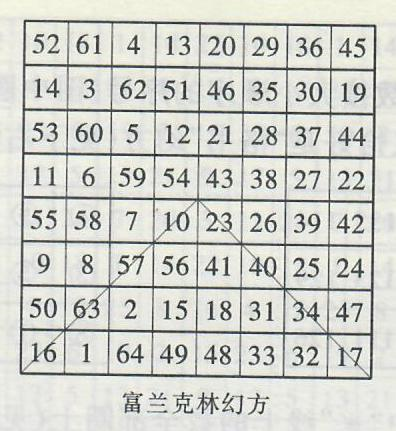
图2
二、幻方的制作
制作幻方是一个古老的游戏,人们不分职业、种族、年龄,都对它乐此不疲。
1.根据数量关系制作幻方
我们先看如何制作一个三阶幻方,讨论下列问题:
在如图3左所示的3×3的方格中填入1~9这9个数,使每行、每列及每条对角线上各数的和分别相等。
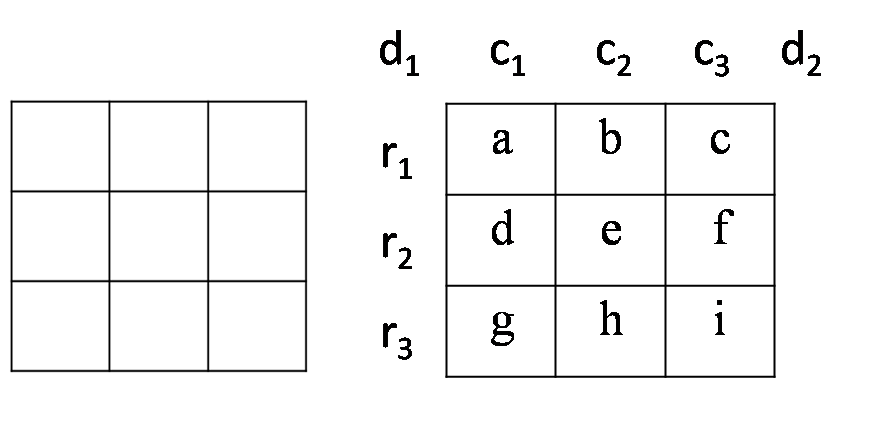
图3
此问题中,每行、每列及每条对角线上各数的和是未知的。要解决此问题,首先必须求出这个相等的和。1~9这9个数的和为9/2(1+9)=45,而共有3行(列),所以每行(列)的和为45/3=15。
如图3右,a~i分别代表数字1~9,r1、r2、r3分别表示相应行的和,c1、c2、c3分别表示相应列的和,d1、d2分别表示相应对角线的和。因为r2+ c2+ d1+ d2=4×15=60,而r2+ c2+ d1+ d2=(d+e+f)+(b+e+h)+(a+e+i)+(c+e+g)=3e+(a+b+c+d+e+f+g+h+i)=3e+45=60,因此e=5,即5应填在幻方的正中间的方格中。由此我们可以立刻得到a+i=g+c=b+h=d+f=15-5=10。
数字1不能填在幻方的角落位置。假设a=1,则i=9。因为2、3、4不能和1在同一行(列)(否则该行或列的和不可能为15),所以剩下的两个位置(h和f所在的位置)要放3个数,这是不允许的,因此1不能填在幻方的角落位置。这样1和9只能被填入某一行(列)的中间位置。
3不能和9在同一行(列),否则该行(列)的第3个数也应是3。
3和7也不能填在幻方的角落位置,否则1与7会在同一行(列),而1与7不能在同一行(列),因为这时该行(列)的另一个数也要是7。
由上面的分析,可以得到如图4所示的8种答案:
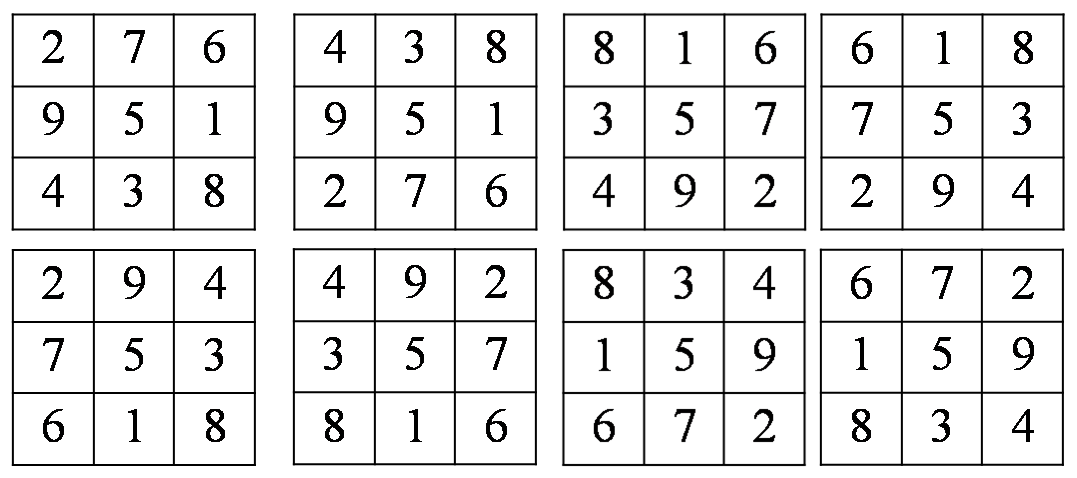
图4
2.奇数阶幻方的制作
(1)三阶幻方的制作
制作一个三阶幻方,先作一个三阶的方形,并且在每边的中间向方形外多作一格(如图5左)。然后,从上一格开始填数字,依着斜线顺序填入,一斜行填好,再填下一斜行,行与行之间保留了一些空格(如图5中)。最后,只要把凸在方形外之格中的数字,分别移到其对面中间的空格中,便构成了一个幻方(如图5右)。
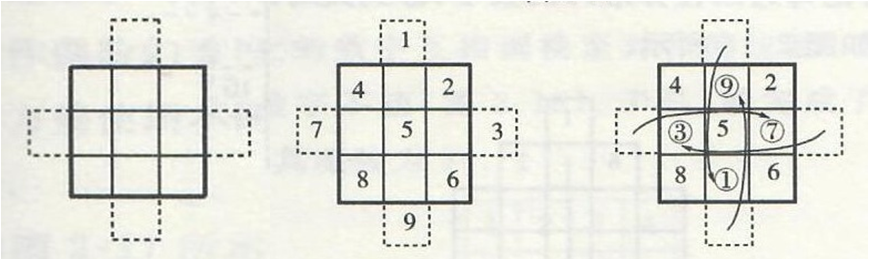
图5
(2)五阶幻方的制作
如图6~7,制作五阶幻方的方法与制作三阶幻方的方法类似。
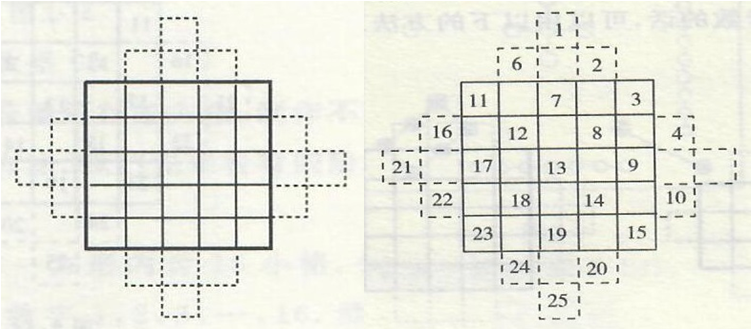
图6
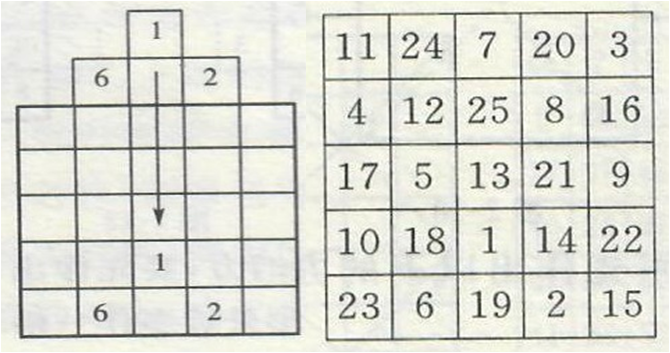
图7
3.偶数阶幻方的制作
(1)四阶幻方的制作
如图8左,作一内含16小格的方形,依次由左开始,每列顺次填入数字1、2、3…16。然后,考虑两对角线上的数字,以方形的中心为对称中心,把对角线上的数字互相调换至对称的位置,不在对角线上的数字不动(如图8中)。于是,就制作成一个四阶幻方(如图8右)。
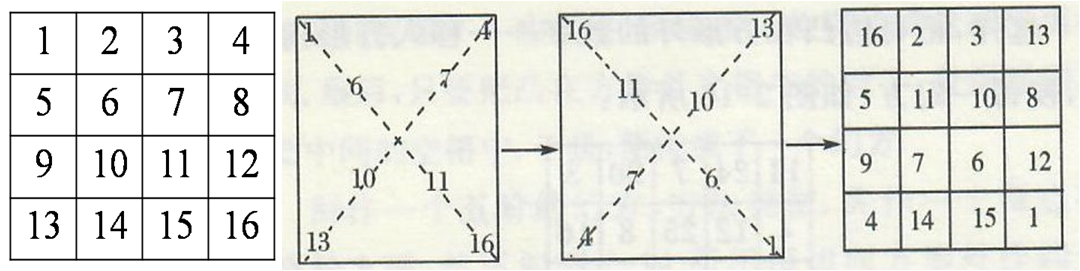
图8
(2)八阶幻方的制作
制作八阶幻方,可先作出如图9所示的方形及特别的斜线,由左上角开始,从左到右,每列依次填上数字,凡数字在斜线经过的格中都特别作了记号。在64格中填好数字后,再调换有记号的数字。调换的方法是以方形的中心点为中心对称点,有记号的数字都要调换到对称的位置。例如,1和64对调;10和55对调;11和54对调;5和60对调;等等。
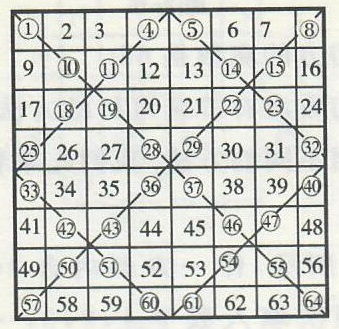
图9
三、具有特殊性质的幻方
1.具有特殊性质的三阶幻方
任意一个三阶幻方都满足:各行(列)所组成的三位数的和及平方和,分别等于各行(列)逆序所组成的三位数的和及平方和。如图10,有
816+357+492=618+753+294,
8162+3572+4922=6182+7532+2942;
834+159+672=438+951+276,
8342+1592+6722=4382+9512+2762。
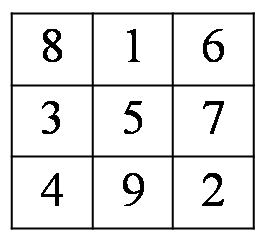
图10
如图11,更神奇的是,若把幻方拼接,位于标识位置的各数字,由它们组成的三位数仍然具有上述性质。例如:
456+312+897=654+213+798,
4562+3122+8972=6542+2132+7982;
258+714+693=852+417+396,
2582+7142+6932=8522+4172+3962。

图11
2.具有特殊性质的四阶幻方
把如图12左所示的四阶幻方沿横向或纵向卷起来再粘上(如图12右),沿任一直线剪开后仍是一个四阶幻方。
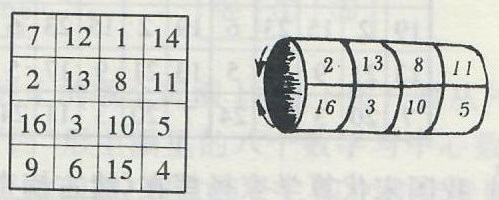
图12
3.具有特殊性质的五阶幻方
如图13所示的五阶幻方具有中心对称性质,即与中心对称的两数之和均为26。

图13
如图14是一个由6个同样的五阶幻方拼接而成的五阶幻方群。有趣的是,从中任取一块5×5的方块(如图中虚线所框)都构成一个五阶幻方。
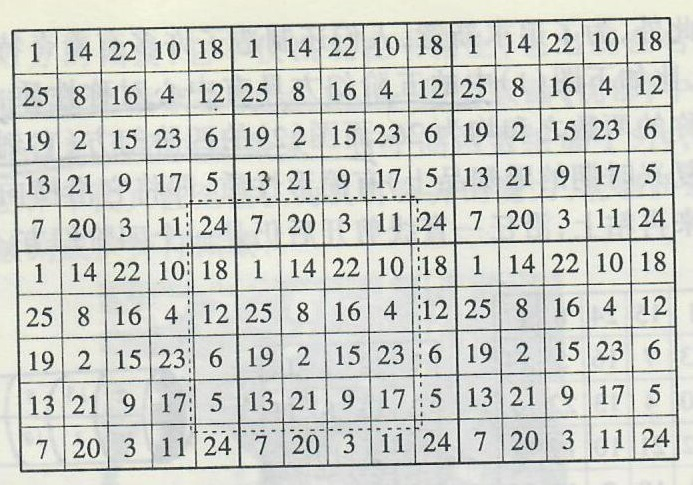
图14
4.具有特殊性质的八阶幻方
日本幻方专家片桐善直制作了如图15上所示的一种奇特的八阶幻方,它是一个“间隔幻方”:相间地从大幻方中取出一些数,可以组成小的幻方。如图15上所示,在八阶幻方中,把用□圈出的数和用○圈出的数分别拿出来,可以得到两个四阶幻方(如图15下)。片桐善直还发现:这种“间隔幻方”共有5760种之多。
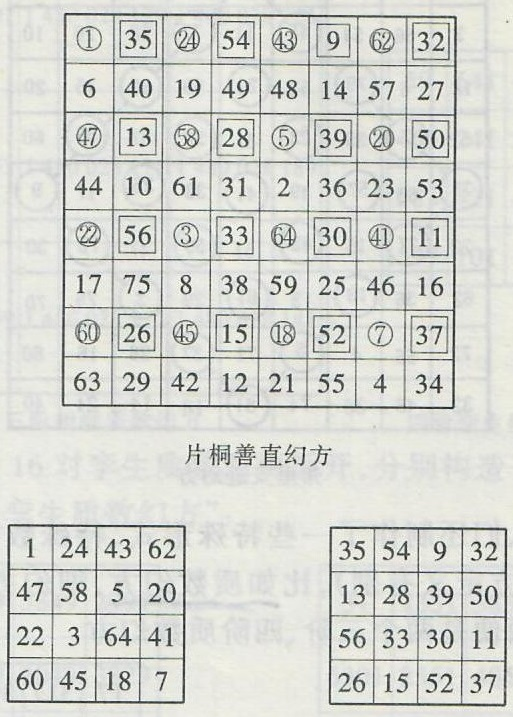
图15
5.具有特殊性质的九阶幻方
我国宋代数学家杨辉在《续古摘奇算法》中给出了如图16所示的九阶幻方。
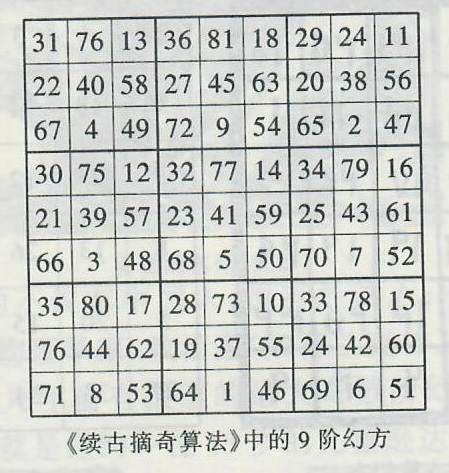
图16
它有如下性质:
(1)以幻方中心41为中心对称的任何位置上的两数之和都为82;
(2)将幻方按如图16中粗线分成9块,可以得到9个三阶幻方;
(3)如图17左所示,若把上述9个三阶幻方的每个幻方的“幻和”值写在九宫格中,则可得到一个新的三阶幻方,且幻方中的9个数构成首项为111、末项为135、公差为3的等差数列。如果将这些数按大小顺序的序号写在九宫格中,则可得到如图17右所示的三阶幻方。
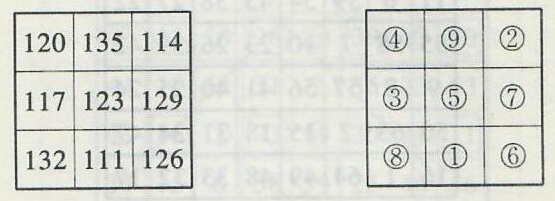
图17
(4)如图18上所示,将幻方中的“米”字线上的数全部圈上,再从外向里分别用方框框上,则每个方框框出的8个数与中心数41可分别构成4个三阶幻方(如图18下)。
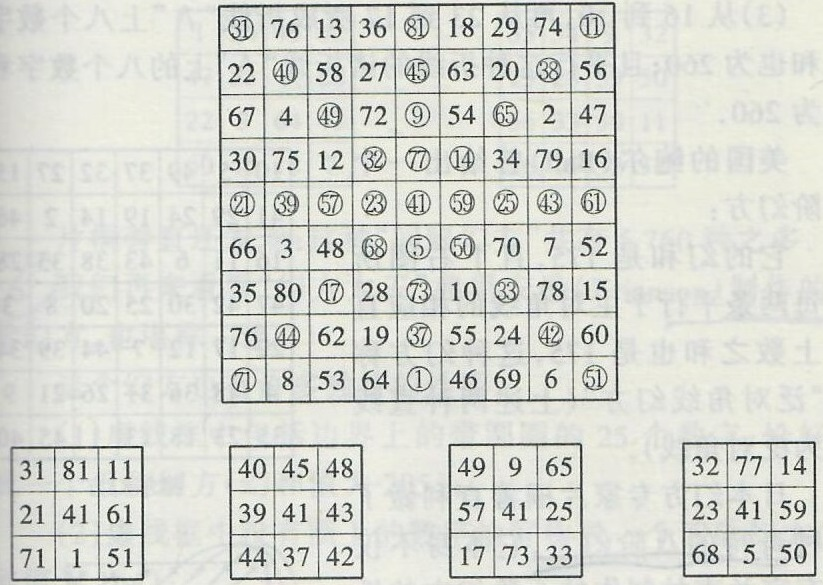
图18
6.质数幻方
上述给出的幻方都是以1,2,3,…等数字作为幻方内的数,其实幻方内的数不一定由1开始,也不必每两个相继的数相差为1,关键是要满足行、列及两条对角线上的数字和均相等。如图19所示的幻方中所有的数均为质数,我们分别称之为三阶、四阶质数幻方。这两个幻方中的数字尾数都相同,一个是9,一个是7。

图19
如图20左是9个相继质数组成的三阶幻方;如图20右是“孪生质数幻方”——幻方中的数皆为孪生质数。

图20
有人还将16对孪生质数两两分开,分别构造了如图21所示的两个四阶幻方——“双孪生质数幻方”。
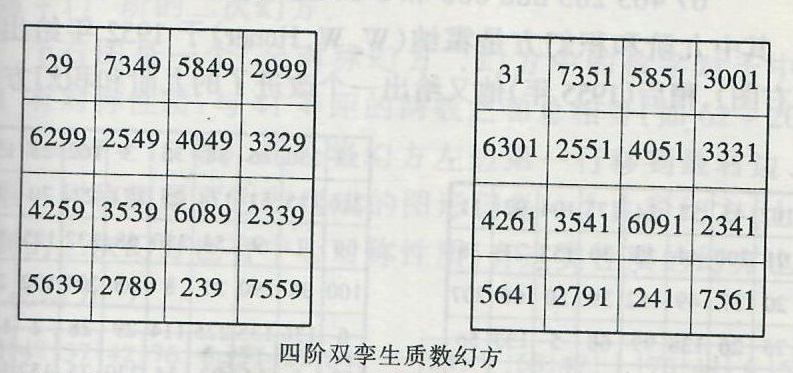
图21
7.天然形成的幻方
从1/19 ~ 18/19这18个分数的小数循环节长度均为18。像图22那样把这18个循环节排成一个18×18的数字阵,刚好构成一个幻方——每行、每列和对角线上的数字之和均为81(严格地说它不是幻方,因为方阵中有相同的数字)。
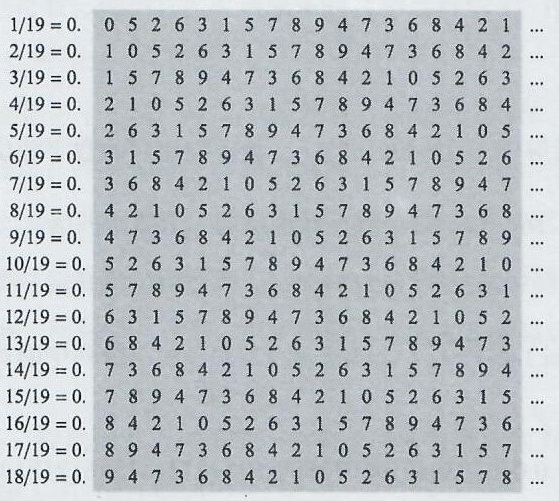
图22
参考文献
[1] 吴振奎,吴旻. 数学中的美[M]. 上海教育出版社,2004:185-199.
[2] 欧阳绛. 数学方法溯源[M]. 大连理工大学出版社,2008:35-40.
[3] 顾森. 思考的乐趣:Matrix67数学笔记[M]. 北京:人民邮电出版社,2012:59.







