李文革
我们试图从“对称”这一直观概念出发,层层深入,逐步揭示“对称”的本质,并通过数学抽象,提炼具有“对称结构”的一类事物的共同特点,从中感受数学的真谛。
一、丰富多彩的对称
在日常生活中我们所理解的“对称”一般是指左右对称和上下对称,如图1所示。

图1
大千世界的对称是丰富多彩的。如图2也给人“对称”的印象。

图2
文学中也有“对称”。例如,北京有一个商号叫“天然居”,挂有“客上天然居,居然天上客”的“回文”牌匾。体育比赛中的循环赛制也含有“对称”的成分。世界杯足球赛决赛阶段是先分组进行循环赛,决出“16强”后再进行淘汰赛。在小组赛阶段,每一个队与小组内所有的队都要进行比赛,这对于各个队是比较平等的、对称的。而淘汰赛阶段,当一个队与某个确定的球队比赛一场后,失败即被淘汰,再没有与其他队比赛的机会了,这对于各个队就不很对称。“不对称”有助于理解“对称”,我们通常所说的“信息不对称”,就是指信息对双方不是对等的。
初中数学教材在轴对称(平面关于一直线的反射)、平移、旋转三种变换的基础上给出了轴对称图形和旋转对称图形的概念:
把一个图形沿某条直线对折,对折后的两部分能完全重合,则称这个图形为轴对称图形。
绕着某个中心旋转一定角度后能与自身重合的图形就称为旋转对称图形。
这两种对称都是平面图形的对称。平面图形的对称还有其他情况。如图3,想象该图案是左右无限延伸的,把它沿水平方向平移一段距离时,得到的图形与原来的图形可以完全重合,这表明该图形是平移对称图形。

图3
如图4,把该图形沿一固定直线方向平移后再沿该直线作反射,得到的图形与原来的图形完全相同,我们称该图形为滑动反射对称图形。
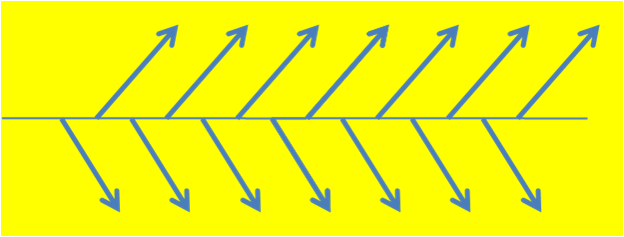
图4
图3和图4称为带饰,是我们生活中经常遇到的图案。
以上这些丰富多彩的“对称”有什么共性?“对称”的本质是什么?如何用数学语言描述“对称”?
二、对称的本质
初中数学教材中的轴对称图形和旋转对称图形概念还“运动”得不够,下面我们从更彻底“运动”的角度看“对称”。
如图5,让等腰三角形所在的平面关于直线l作反射,这时平面上的点都运动起来了,如果点P变到点P',点P'变到点P,则点P、P'关于直线l为轴对称。这时等腰三角形上的点都运动起来了,如果等腰三角形上所有点的集合在反射前后仍然是原来的集合,则称该等腰三角形关于直线l为轴对称。在这一变化过程中,等腰三角形上的点都运动起来了,但整个等腰三角形却没有改变。
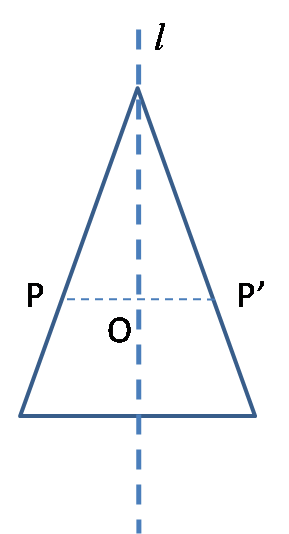
图5
如图6,把等边三角形绕着点O逆时针旋转120°时,平面上的点都在运动变化,该等边三角形上的点也在运动变化,但等边三角形在运动变化中整体未变,则称该等边三角形关于点O为旋转对称图形。
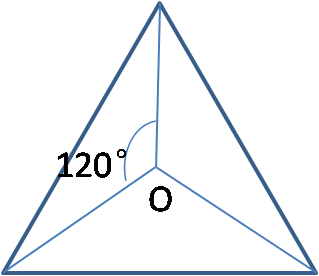
图6
可以证明,关于平面图形的对称,有且只有反射对称、旋转对称、平移对称、滑动反射对称这四类运动变换及相应的四类对称。这四类运动变换都保持图形的形状和大小不变,我们称之为刚体运动变换,或称保距变换:保持平面上任意两点间的距离在运动前后不变。平面不动也可以看成是一种保距变换,它可以看成平面旋转0°或平移a=0的保距变换,通常称为恒等变换。
我们把所有使平面图形T整体不变的保距变换放在一起构成一个集合,记着G(T),并称G(T)为T的对称集,其元素个数记着|G(T)|。例如正方形T',关于两条对角线、两条对边中点的连线的反射下整体不变,绕其中心逆时针旋转0°、90°、180°、270°时也整体不变,因此,G(T')的元素的个数为8,即|G(T')|=8。
研究平面图形的对称,就是要研究平面图形作为整体在保距变换下的不变性,并据此判断和衡量该平面图形的对称性。例如,对正三角形T"来说,易得|G(T")|=6<|G(T')|=8,说明正三角形的对称性弱于正方形的对称性。
三、用数学语言描述对称
G(T)中的元素是所有保持平面图形T整体不变的保距变换,包括反射、旋转、平移、滑动反射四种,它们有两个特点:都是平面上的保距变换;保持T整体不变。这四种保距变换还可以“相继实施”,比如,先平移后反射,同一种变换也可以实施几次。我们把这种保距变换的“相继实施”称为G(T)中的元素的一种“运算”,记着“*”,叫做“乘法”。例如“a*b”,表示先实施保距变换b,再实施保距变换a。这种乘法满足以下四条规律:
(1)封闭律
若a∈G(T),b∈G(T),则 a*b∈G(T)。
(2)结合律
若a∈G(T),b∈G(T) ,c∈G(T),则(a*b)*c=a*(b*c)。
(3)幺元律
对任意的a∈G(T),存在i ∈G(T),使i*a=a*i=a。i实际上就是恒等变换。
(4)逆元律
对任意的a∈G(T),存在a'∈G(T),使a*a'=a'*a=i。a'称为a的逆元。
以上表明,平面图形T的对称集G(T)是一个有结构的集合:G(T)的元素有运算,并且该运算满足封闭律、结合律、幺元律、逆元律。具有满足这种性质的结构的集合G(T)就构成了一个群,称为平面图形T的对称变换群。
如图7,正三角形的每个对称变换都把它的三个顶点变为这三个顶点的一个排列,这样我们可以用顶点的变化来描述正三角形的每个对称变换。例如,如图7右,正三角形绕中心逆时针旋转120°,就相当于把3个数字“1、2、3”变为它的一个排列“2、3、1”。
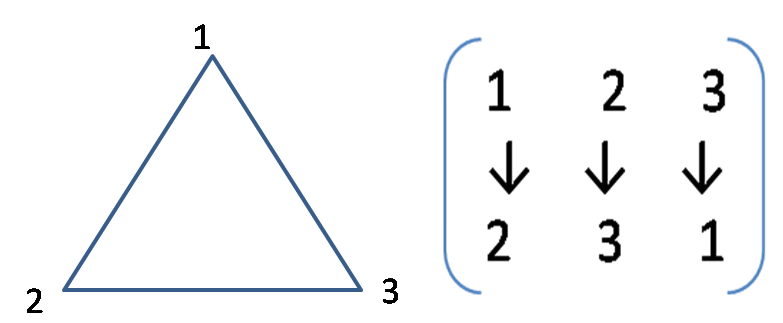
图7
去掉图7右中的箭头,我们可以写出正三角形T"的对称集G(T")的所有元素如下:
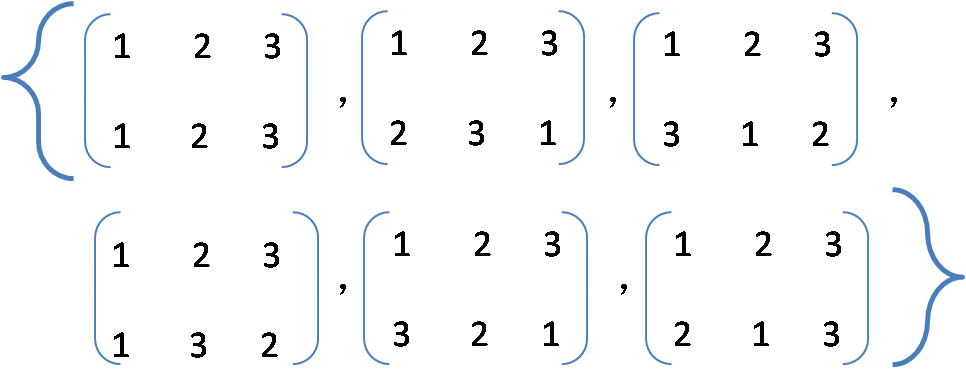
我们可以“计算”出G(T")中元素的运算结果,例如可以得出

有了群这个数学武器,关于它的种种性质都可以应用到各种“对称”上去,从而深化了我们对“对称”的认识。群论正是试图提炼具有“对称结构”的一类事物的共同特点,从而把握客观世界某一方面的本质。例如,有了群论,我们可以用统一的观点看待各种几何学。欧氏几何就是研究在刚体运动变换群下图形的不变性质;仿射几何就是研究在仿射变换下图形的不变性质;射影几何就是研究在射影变换下图形的不变性质。这使我们深切感受到:数学是关于模式和结构的科学!
四、数学“来源于实践又应用于实践”
前面我们提到的带饰,就是平移对称或滑动反射对称的图形。如图8是带饰的一些例子。

图8
带饰的对称性群称为“带饰群”。不同的带饰可以有本质上相同的对称性,从而有相同的带饰群。也就是说,带饰图案可能千差万别,但在“对称结构”上可能是相同的。用“群”的知识可以证明:带饰群只有7个,其“对称结构”示意图如图9所示。
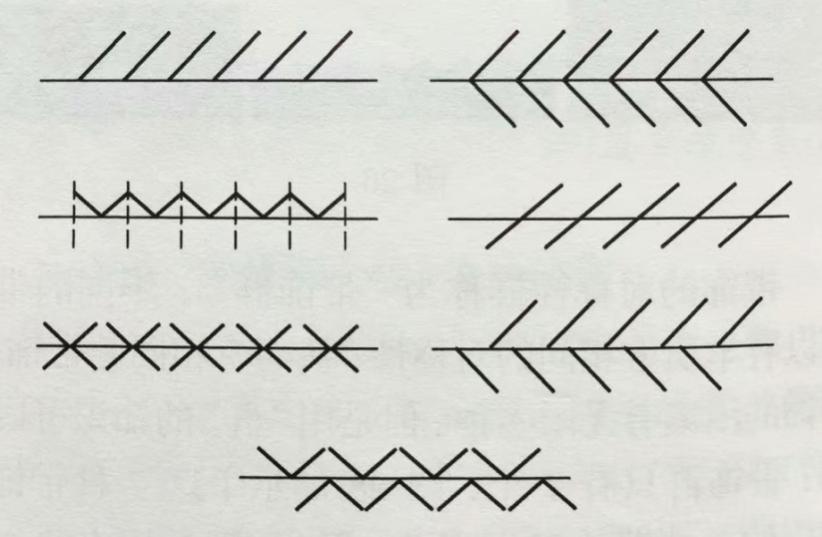
图9
面饰是在两个相交方向上都是平移对称或滑动反射对称的图形。如图10是面饰的一些例子。

图10
类似地,面饰的对称性群称为“面饰群”。利用“群”的知识可以证明:面饰群只有17个,其“对称结构”示意图如图11所示。

图11
这样,在进行壁纸设计时,只需要17个计算机程序,就可以设计出所有的壁纸来,而需要调整的只是“面饰单元”(如图12所示)。
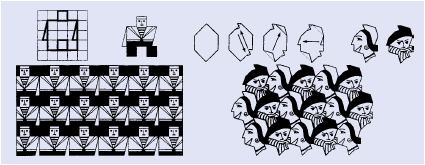
图12
参考文献
顾沛. 对称与群[M]. 北京:高等教育出版社,2013.







